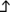heinz hat geschrieben: 
04.01.2019 21:54:18
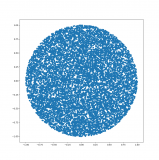
Leider sind die Positionen nicht richtig gleichmaessig verteilt
Zuerst mal zu radius.
So wie du es gebaut hast, gibt das eine Gleichverteilung auf die 2000-Elementige Punktemenge {0.0, ..., 199.9}. In der Fläche betrachtet ist das nicht gleichmäßig, denn 187.6 kommt genauso häufig vor wie 3.4, aber der Ring mit Radius 187.6 plusminus 0.05 hat viel mehr Fläche als der Ring mit Radius 3.4 plusminus 0.05, und es landen gleich viele Punkte in den Ringen. Wenn du die Ringe auseinanderwickelst, hast du nahezu Rechtecke mit Kantelnänge 187.6*2*π und 0.1 und Kantenlänge 3.4*2*π und 0.1. (π habe ich mit mit Strg+Shift+u 3c0 Enter geschrieben, nachdem ich nachgeschaut habe, dass das das Unicodezeichen U+03C0 ist.) Du musst das passend strecken. Genau das machst du bei der Substitution im Integral, wenn du von kartesischen Koordinaten auf Polarkoordinaten wechselst, und dabei der Radius als Steckfaktor (Determinante der Ableitung der Transformation) auftaucht.
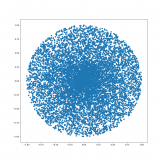
Mich erinnert das an "π mit Montecarlo berechnen" aus der Reihe "Viele Möglichkeiten, π zu bestimmen". Da schießt man n mal gleichverteilt mit x zwischen -1 und 1 und y zwischen -1 und 1, dann zählt man die Treffer, wo x^2+y^2 < 1 ist, sei das t. Dann ist, weil der Kreis Fläche π hat, und das Quadrat die Fläche 4, π=4*t/n.
So könntest du es auch machen: x und y gleichverteilt wählen, und wenn x^2+y^2 > 1 ist, wegschmeißen.
Nun zu winkel.
Ich habe mal herumgespielt, Folgendes gemacht.
Code: Alles auswählen
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main ()
{
int a=0;
int b=0;
int c=100000000;
for (int z=0; z<c; z++)
{
float winkel= (float) (rand()% 36000000) / 100000.0;
float s= sin(winkel * (M_PI / 180.0));
if ( s == 0.0 ) printf("Eine Null!\n");
if (s > 0.0 && s < 0.1) a++;
if (s > 0.1 && s < 0.2) b++;
}
printf("%d: %d %d\n",c,a,b);
}
Ergebnis
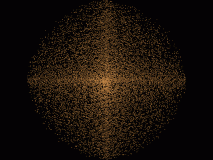
Demnach ist der Sinus nicht ungewöhnlich häufig nahe bei 0. Das scheint mir ein Artefakt bei der grafischen Darstellung zu sein.
Wie hast du die Grafik gemacht?