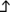Probleme beim Zufalls-Punkte erzeugen [gelöst]
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
also was man schon sieht, ist ja dass x und y jeweils von 3 zufallszahlen abhängt aber z nur von zweien.
Und wenn man aus der Z Richtung drauf schaut, schauts ja gut aus.
Aber mir leuchtet das nicht ein warum das einen unterschied machen sollte...
Und wenn man aus der Z Richtung drauf schaut, schauts ja gut aus.
Aber mir leuchtet das nicht ein warum das einen unterschied machen sollte...
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Ok, 3 histogramme (dichteschätzer) sind besser als einersmutbert hat geschrieben:11.01.2019 20:56:43hab das einmal in r nachgestellt und im Histogramm ist der Unterschied deutlich zu sehen. Zum Nachdenken wieso bin ich noch nicht gekommen...
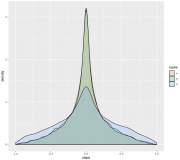
Gibt es eigentlich eine Möglichkeit Kreis oder Kugelkoordinaten (oder sagen wir n-dimensionale koordinaten) in einer einzigen Zahl zusammenzufassen? Gibt es da eine Ordnung die zB Koordinaten in Rationale Zahlen umbaut?
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Beachte die Fläche auf der Kugel zwischen dem theta-ten und dem (theta + epsilon)-ten Breitengrad!reox hat geschrieben:11.01.2019 16:49:02Also es schaut so aus, als ob die Verteilung an den Polen größer ist. Nur warum? Offenbar erzeugt die Verteilung von phi und radius das erwartete Bild. Nur theta scheint nicht das zu tun was wir erwarten.Code: Alles auswählen
theta = np.pi * np.random.rand(N) phi = 2 * np.pi * np.random.rand(N) radius = r * np.random.rand(N) x = np.sin(theta) * np.cos(phi) * radius; y = np.sin(theta) * np.sin(phi) * radius; z = np.cos(theta) * radius
Das hängt von theta ab. Je näher am Pol, desto kleiner diese Fläche.
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
@heinz
Darf man zwischendurch einmal fragen wie die Verteilung aussehen soll?
Die größere Dichte in der Mitte ist gewünscht?
(Entschuldige, falls es schon im Thread steht, aber ich hab nichts gefunden.)
Darf man zwischendurch einmal fragen wie die Verteilung aussehen soll?
Die größere Dichte in der Mitte ist gewünscht?
(Entschuldige, falls es schon im Thread steht, aber ich hab nichts gefunden.)
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Ich denke, dass die Verteilung über eine Kugelsphäre gleich sein soll. Das mit dem Radius soll unabhängig davon sein.smutbert hat geschrieben:15.01.2019 12:53:03Darf man zwischendurch einmal fragen wie die Verteilung aussehen soll?
Die größere Dichte in der Mitte ist gewünscht?
Mit theta=pi*Zufall (Zufall ist gleichverteilt auf [0,1]) haut das nicht hin, weil ein Breitengrad die Länge radius*2*pi*sin(theta) hat. Die Verteilung der theta muss so sein, dass das bei gleichem Radius eine gleiche Verteilung auf der Kugelsphäre ergibt.
Nun ist in jedem Punkt der Kugelsphäre der Winkel zwischen dem Meridian und der Ebene parallel zum Äquator ebenfalls theta, also bei Veränderung des theta das Verhältnis von der Änderung in z-Richttung zur Änderung des theta sin(theta). Wenn man auf der z-Achse gleichverteilt, und das dann auf den Meridian abbildet, passt es. Also ist theta=acos(2*Zufall - 1) passend.
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Danke erstmal an diejenigen die sich noch gedanken ueber diese "Sache" machen.

und von der Seite
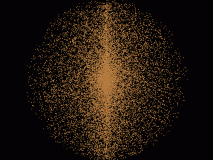
gleich aussehen wuerde, also keine "seltsamen" Anhaufungen ausser die im Zentrum.
MMn. ist die groessere Dichte in der Mitte eine andere Baustelle um die ich mich noch nicht gekuemmert habe.
Es wurde ja schon von hikaru geschrieben:
Für eine gleichmäßige Dichte in der Fläche musst du dafür sorgen, dass deine Punkte gleichmäßig auf dem Quadrat des Radius' verteilt sind.
Nach meinem Verstaendnis, je groesser der Radius um so groesser die Wahrscheinlichkeit fuer einen gesetzten Punkt. (Quadratisch zunehmend)
(Vlt. eine rand-Funktion die (Quadratisch) mehr grosse Zahlen (Radien) liefert als kleine.)
Ich denke/hoffe, das bekomme ich hin. Wollte nur erst mal die eine "Baustelle" beenden, bevor ich mit der naechsten beginne.
Aber Du hast recht, die 3 Radien (x,y,z) sollen einzeln bestimmbar sein.
Viele Gruesse,
heinz
Ich wäre schon zufrieden wenn die Betrachtung von obensmutbert hat geschrieben:15.01.2019 12:53:03Darf man zwischendurch einmal fragen wie die Verteilung aussehen soll?
Die größere Dichte in der Mitte ist gewünscht?

und von der Seite

gleich aussehen wuerde, also keine "seltsamen" Anhaufungen ausser die im Zentrum.
MMn. ist die groessere Dichte in der Mitte eine andere Baustelle um die ich mich noch nicht gekuemmert habe.
Es wurde ja schon von hikaru geschrieben:
Für eine gleichmäßige Dichte in der Fläche musst du dafür sorgen, dass deine Punkte gleichmäßig auf dem Quadrat des Radius' verteilt sind.
Nach meinem Verstaendnis, je groesser der Radius um so groesser die Wahrscheinlichkeit fuer einen gesetzten Punkt. (Quadratisch zunehmend)
(Vlt. eine rand-Funktion die (Quadratisch) mehr grosse Zahlen (Radien) liefert als kleine.)
Ich denke/hoffe, das bekomme ich hin. Wollte nur erst mal die eine "Baustelle" beenden, bevor ich mit der naechsten beginne.
Am Ende waere ich froh, beides zu haben (an-/abschaltbar), einmal mit haeufung bei kleinen Radien und einmal ohne.Lohengrin hat geschrieben:17.01.2019 22:38:27Ich denke, dass die Verteilung über eine Kugelsphäre gleich sein soll. Das mit dem Radius soll unabhängig davon sein.
Aber Du hast recht, die 3 Radien (x,y,z) sollen einzeln bestimmbar sein.
Viele Gruesse,
heinz
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
So habe ich es jetzt probiert, allerdings wieder in r, weil es zu lange dauert bis ich in C etwas lauffähiges hinbekomme (falls ich es überhaupt schaffe):
Damit berechne ich, wie Logengrinn es geschrieben hat, Punkte, die auf der Oberfläche eines Ellipsoids gleich(mäßig) verteilt sind.
runif erzeugt gleich verteilte Zufallszahlen zwischen 0 und 1, das heißt da kommen Vektoren mit der Länge N (50) heraus. Mit dem letzten Befehl wird das Ergebnis geplottet, allerdings erscheint es wieder als Kugel, weil die Achsen einzeln automatisch skaliert werden (und ich habe es auf die Schnelle nicht geschafft die Skalierung fix vorzugeben).
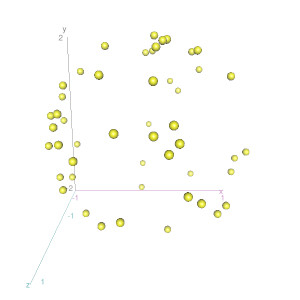
Um nun das ganz Volumen gleichmäßig mit Punkten zu füllen, führe ich das ganze in einer Schleife aus und zwar mit einem Skalierungsfaktor, den ich mit den Werten im Beispiel in Hundertstelschritten von 1/100 bis 1 durchlaufen lasse und plotte jedes Mal die erzeugten Punkte.
Mit N=10 und den Nr=100 Skalierungsfaktoren sollten am Ende 1000 Punkte herauskommen.

Es gibt keine bevorzugte Richtung mehr. Innen häufen sich die Punkte, weil bei den früheren Schleifendurchläufen trotz kleinerem Skalierungsfaktor/Radius gleich viele Punkte gibt wie bei den späteren Schleifendurchgängen. Ohne es jetzt genau durchdacht zu haben, wird man die Häufung los, indem man das Quadrat des Skalierungsfaktors in die Zahl der Zufallszahlen pro Schleifendurchgang einfließen lässt
(das mit N*scale^2 als Anzahl der Zufallszahlen funktioniert in r, anderswo müsste man diese Zahl wohl auf einen Integerwert runden)

In weiterer Folge könnte man die Abhängigkeit der Dichte vom Radius beliebig ändern, zum Beispiel normalverteilte Zufallszahlen erzeugen und die dann als Skalierungsfaktoren verwenden oder ähnliches.
Code: Alles auswählen
library("scatterplot3d")
library("car")
N=50
rx=1
ry=2
rz=1.5
phi=2*pi*runif(N)
theta=acos(2*runif(N)-1)
x=rx*cos(phi)*sin(theta)
y=ry*sin(phi)*sin(theta)
z=rz*cos(theta)
scatter3d(x, y, z, surface=FALSE)
runif erzeugt gleich verteilte Zufallszahlen zwischen 0 und 1, das heißt da kommen Vektoren mit der Länge N (50) heraus. Mit dem letzten Befehl wird das Ergebnis geplottet, allerdings erscheint es wieder als Kugel, weil die Achsen einzeln automatisch skaliert werden (und ich habe es auf die Schnelle nicht geschafft die Skalierung fix vorzugeben).

Um nun das ganz Volumen gleichmäßig mit Punkten zu füllen, führe ich das ganze in einer Schleife aus und zwar mit einem Skalierungsfaktor, den ich mit den Werten im Beispiel in Hundertstelschritten von 1/100 bis 1 durchlaufen lasse und plotte jedes Mal die erzeugten Punkte.
Mit N=10 und den Nr=100 Skalierungsfaktoren sollten am Ende 1000 Punkte herauskommen.
Code: Alles auswählen
library("rgl")
N=10
Nr=100
rx=1
ry=2
rz=1.5
for(i in 1:Nr) {
scale=i/Nr
phi=2*pi*runif(N)
theta=acos(2*runif(N)-1)
x=scale*rx*cos(phi)*sin(theta)
y=scale*ry*sin(phi)*sin(theta)
z=scale*rz*cos(theta)
plot3d(x, y, z, add=TRUE)
}

Es gibt keine bevorzugte Richtung mehr. Innen häufen sich die Punkte, weil bei den früheren Schleifendurchläufen trotz kleinerem Skalierungsfaktor/Radius gleich viele Punkte gibt wie bei den späteren Schleifendurchgängen. Ohne es jetzt genau durchdacht zu haben, wird man die Häufung los, indem man das Quadrat des Skalierungsfaktors in die Zahl der Zufallszahlen pro Schleifendurchgang einfließen lässt
Code: Alles auswählen
library("rgl")
N=20
rx=1
ry=2
rz=1.5
Nr=100
for(i in 1:Nr) {
scale=i/Nr
phi=2*pi*runif(N*scale^2)
theta=acos(2*runif(N*scale^2)-1)
plot3d(scale*rx*cos(phi)*sin(theta), scale*ry*sin(phi)*sin(theta), scale*rz*cos(theta), add=TRUE)
}

In weiterer Folge könnte man die Abhängigkeit der Dichte vom Radius beliebig ändern, zum Beispiel normalverteilte Zufallszahlen erzeugen und die dann als Skalierungsfaktoren verwenden oder ähnliches.
Zuletzt geändert von smutbert am 19.01.2019 20:39:50, insgesamt 1-mal geändert.
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Ja, du brauchst eine Zufallsvariable, die eine Verteilung hat, wo die Wahrscheinlichkeitsdichte quadratisch wächst.heinz hat geschrieben:18.01.2019 19:12:31Nach meinem Verstaendnis, je groesser der Radius um so groesser die Wahrscheinlichkeit fuer einen gesetzten Punkt. (Quadratisch zunehmend)
(Vlt. eine rand-Funktion die (Quadratisch) mehr grosse Zahlen (Radien) liefert als kleine.)
So etwas kannst du aus einer Gleichverteilung auf [0,1] erzeugen, indem zu das mit etwas Passendem auf [0,R] abbildest.
Ein Fachbegriff dazu ist Bildmaß. Eine Verteilung (zB Gleichverteilung auf [0,1]) wird durch die Zufallsvariable auf einen anderen Bereich (zB [0,R]) übertragen.
Auf diese Tour kann man auch Verteilungen erzeugen, die so sind, wie etwas, das man gerade gemessen hat. Wenn man zB tausend Messwerte hat, kann man sich 500 davon zufällig auswählen, damit die passende Zufallsvariable bauen, und dann mit Zufallswerten, die so sind wie diese 500, an den anderen 500 herumspielen. Aber man darf da nicht zu viel hineininterpretieren. Wenn man Pech hat, waren die einen 500 und die anderen 500 doch nicht voneinander unabhängig, man publiziert eine Sensation, und dann korreliert das doch nur mit dem Fahrplan der Straßenbahn (pünktlich alle 10 Minuten hat da was vibriert).
Wenn du etwas haben willst, wo "größeres aus [0,1] auf größeres in [0,R]" gilt, gibt es nur eine Lösung.
Beim Kreis (2-dimensional) geht das mit Wurzel.
Beweis: 0 wird auf 0 abgebildet, 1 auf R. Irgend ein x wird auf r abgebildet, also das Stück [0,x] auf das Stück [0,r]. Das Verhältnis der Kreisflächen mit r und R ist (r/R)^2. Im Kreis mit Radius r soll (r/R)^2 der Punkte liegen. Weil bei Gleichverteilung auf [0,1] das Stück von [0,(r/R)^2] das Gewicht (r/R)^2 hat, muss x=(r/R)^2 auf r abgebildet werden. Nach r aufgelöst ergibt das r=R*Wurzel(x).
Bei der Kugel (3-dimensional) geht es genauso. Das Verhältnis der Volumen mit Radius r und R ist (r/R)^3. Also muss x=(r/R)^3 auf r abgebildet werden. Nach r aufgelöst ergibt das r=R*Kubikwurzel(x).
Was für drei Radien? Meinst du drei Radien vom Ellipsoid?heinz hat geschrieben:18.01.2019 19:12:31Am Ende waere ich froh, beides zu haben (an-/abschaltbar), einmal mit haeufung bei kleinen Radien und einmal ohne.Lohengrin hat geschrieben:17.01.2019 22:38:27Ich denke, dass die Verteilung über eine Kugelsphäre gleich sein soll. Das mit dem Radius soll unabhängig davon sein.
Aber Du hast recht, die 3 Radien (x,y,z) sollen einzeln bestimmbar sein.
Das mit acos für theta geht nur, wenn das eine Kugel ist. Wenn du die Kugel verzerrst, dann hast du in jedem Ellipsoidsektor so viele Punkte, wie es der Raumwinkel der Elipsoidsphäre verlangt, und das ist dann je nach Richtung verschieden großes Volumen. Du müsstest da je nach Raumwinkel unterschiedlich viel reinwerfen.
Ich empfehle immernoch Montecarlo. Gleichverteilung im Raum geht mit kartesischen Koordinaten ganz leicht. Und was draußen liegt, ist leicht zu erkennen.
Die sind auf den Raumwinkeln gleichmäßig verteilt. Auf der Fläche sind sie es nicht, weil du die Kugel verzerrt hast.smutbert hat geschrieben:18.01.2019 23:32:42Damit berechne ich, wie Logengrinn es geschrieben hat, Punkte, die auf der Oberfläche eines Ellipsoids gleich(mäßig) verteilt sind.
Wenn du es geschafft hast, Gleichverteilung auf einer Ellipsoidsphäre zu bauen, passt es im Volumen wieder nicht, weil je nach Richtung die Schalen unterschiedlich dicht liegen.
Dass du theta und phi vertauscht hast, könnte verwirren.
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Danke für die Erklärungen. Ich habe mir beim Übergang von der Kugel zu dem Ellipsoid zu wenig (eigentlich gar nichts) gedacht. (zumindest habe ich jetzt das phi/theta-Chaos aufgeräumt)
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
@Lohengrin
Danke nochmals fuer die ausfuehrliche Erklaerung!
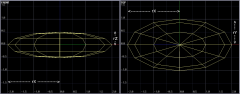
Ich hoffe so wird es "klarer" was ich meine...
Mein Ziel ist ein Ellipsoid.
Der Kreis scheint mir verstaendlich.
Allerdings scheitere ich daran, zu verstehen was im Zusammenhang mit dem Ellipsoid a,b und c ist.
Sind das die max. Radius-Werte? Also z.B. a=2000; b=1000; c=500;?
Falls ja, muessten die Radien dann nicht auch in der Kreis-Formel auftauchen?
z.B. (z0/a)^2+(z1/b)^2 < 1
Gruss, heinz
Danke nochmals fuer die ausfuehrliche Erklaerung!
rX=2000; rY=1000; rZ=500Lohengrin hat geschrieben:19.01.2019 12:20:43Was für drei Radien? Meinst du drei Radien vom Ellipsoid?

Ich hoffe so wird es "klarer" was ich meine...
Und ein paar Posts vorher:
das wollte ich versuchen umzusetzen.Lohengrin hat geschrieben:Kreis ...Du nimmst solange zwei Zufallszahlen z0 und z1 zwischen 0 und 1, bis z0^2+z1^2 < 1
Ellipsoid geht genauso. Da wiederholst du, bis du (z0/a)^2+(z1/b)^2+(z2/c)^2 < 1 hast.
Mein Ziel ist ein Ellipsoid.
Der Kreis scheint mir verstaendlich.
Allerdings scheitere ich daran, zu verstehen was im Zusammenhang mit dem Ellipsoid a,b und c ist.
Sind das die max. Radius-Werte? Also z.B. a=2000; b=1000; c=500;?
Falls ja, muessten die Radien dann nicht auch in der Kreis-Formel auftauchen?
z.B. (z0/a)^2+(z1/b)^2 < 1
Gruss, heinz
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Das habe ich falsch, mindestens verwirrend, erklärt.heinz hat geschrieben:21.01.2019 17:07:03das wollte ich versuchen umzusetzen.Lohengrin hat geschrieben:Kreis ...Du nimmst solange zwei Zufallszahlen z0 und z1 zwischen 0 und 1, bis z0^2+z1^2 < 1
Ellipsoid geht genauso. Da wiederholst du, bis du (z0/a)^2+(z1/b)^2+(z2/c)^2 < 1 hast.
Mein Ziel ist ein Ellipsoid.
Der Kreis scheint mir verstaendlich.
Allerdings scheitere ich daran, zu verstehen was im Zusammenhang mit dem Ellipsoid a,b und c ist.
Sind das die max. Radius-Werte? Also z.B. a=2000; b=1000; c=500;?
Beim Kreis habe ich z0 und z1 aus dem Bereich von 0 bis 1 genommen.
Beim Ellipsoid habe ich z0 aus dem Bereich von -a bis a, z1 aus dem Bereich von -b bis b und z2 aus dem Bereich von -c bis c gemeint.
Du kannst einen Ellipsoid erzeugen, wenn du die Einheits-Kugel streckst. Streckst du in alle drei Richtungen gleich, also a=b und b=c, dann wird es eine Kugel.
Wenn du etwas in den Raum streust, und wissen willst, ob es im Ellipsoid ist, dann machst du die Streckung wieder rückgängig, und schaust, ob das dann in der Einheitskugel ist.
Beim Kreis ist a=b, wird da üblicherweise R genannt. (Das ist jetzt genau der Mathematikerwitz "Beweis durch Verwirrung": Sei a gleich b, wir nennen es c.) Aus (z0/a)^2+(z1/b)^2 < 1 wird dann (z0/R)^2+(z1/R)^2 < 1, mit "mal R^2" äquivalent umgeformt ergibt das z0^2+z1^2 < R^2, also "(z0,z1) liegt in Kugel mit Radius R" gemäß Pythagoras (Beachte das Dreieck mit den Eckpunkten (0,0), (z0,0), (z0,z1). Der rechte Winkel ist bei (z0,0), die lange Seite ist von (0,0) nach (z0,z1), Länge R.).heinz hat geschrieben:21.01.2019 17:07:03Falls ja, muessten die Radien dann nicht auch in der Kreis-Formel auftauchen?
z.B. (z0/a)^2+(z1/b)^2 < 1
Um einen gleichmäßig gefüllten Ellipsoid zu bauen, kannst du z0,z1,z2 aus dem Bereich von -1 bis 1 wählen, und mitnehmen, wenn z0^2+z1^2+z2^2 < 1. Dann hast du eine gefüllte Einheitskugel. Das streckst du dann zum Ellipsoid, also (z0,z1,z2) wird zu (a*z0, b*z1, c*z2).
Du kannst aber auch z0 aus dem Bereich von -a bis a, z1 aus dem Bereich von -b bis -b und z2 aus dem Bereich von -c bis c nehmen. Dann hast du erst einmal einen gleichmäßig gefüllten Quader. Du nimmst den Punkt mit, wenn er im Ellipsoid liegt, also wenn (z0/a)^2 + (z1/b)^2 + (z2/c)^2 < 1.
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Ich hoffe, ich habe es jetzt kapiert.
Der Code sieht jetzt so aus:
 40591
40591
Ist das so wie Du es meintest?
(Ups: > mit < verwechselt...)
Die Werte, die dabei entstehen:
 40590
40590
Und aussehen tut es jetzt so:
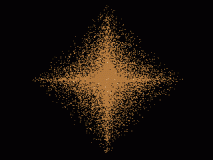
(Ist wieder ein animiertes .gif Rotiert um die x- und y-Achse
Die x-, y- und z-Radius-Werte sind alle gleich damit eine Kugel entsteht.
Die Kamera blickt von oben drauf.)
Ersetze ich:
durch
Sieht es so aus:
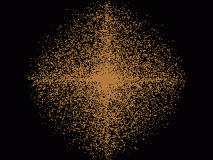
Es ist zum Maeusemelken...
Gruss, heinz
Der Code sieht jetzt so aus:
Ist das so wie Du es meintest?
(Ups: > mit < verwechselt...)
Die Werte, die dabei entstehen:
Und aussehen tut es jetzt so:

(Ist wieder ein animiertes .gif Rotiert um die x- und y-Achse
Die x-, y- und z-Radius-Werte sind alle gleich damit eine Kugel entsteht.
Die Kamera blickt von oben drauf.)
Ersetze ich:
Code: Alles auswählen
while(rX*rX + rY*rY + rZ*rZ > 1.0);Code: Alles auswählen
while(rX*rX + rY*rY + rZ*rZ < 1.0);
Es ist zum Maeusemelken...
Gruss, heinz
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Warum die Winkel? Lass das weg!
macht solange einen Punkt (rX,rY,rZ) in den Würfel [-1,1]x[-1,1]x[-1,1], bis (rX,rY,rZ) in der Einheitskugel liegt.
Das steckst du dann.
Das Ergebnis ist ein Punkt (XX,YY,ZZ) im Ellipsoid
Code: Alles auswählen
do
{
rX=(double)(rand()%20000000 - 10000000)/10000000.0;
rY=(double)(rand()%20000000 - 10000000)/10000000.0;
rZ=(double)(rand()%20000000 - 10000000)/10000000.0;
}
while(rX*rX + rY*rY + rZ*rZ > 1.0);
Das steckst du dann.
Code: Alles auswählen
XX=radX*rX;
YY=radY*rY;
ZZ=radZ*rZ;
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Lieber Lohengrin ,
ES FUNKTIONIERT!
Vielen herzlichen Dank fuer Deine Geduld und Deine ausdauernde Hilfe!
Auch nochmals vielen Dank an alle anderen, die sich damit beschaeftigt haben.
Gruss, heinz
Falls es sonst noch jemanden interessiert, hier ist die endgueltige Loesung:
 40592
40592
ES FUNKTIONIERT!
Sorry, das ich so lange gebraucht habe um es zu kapieren...
Vielen herzlichen Dank fuer Deine Geduld und Deine ausdauernde Hilfe!
Auch nochmals vielen Dank an alle anderen, die sich damit beschaeftigt haben.
Gruss, heinz
Falls es sonst noch jemanden interessiert, hier ist die endgueltige Loesung:
Re: Probleme beim Zufalls-Punkte erzeugen [aufgegeben]
Ja die Lösung hatten wir ja auch schon für 2D. Interessant wäre es jetzt so eine Lösung zu machen ohne das man Werte wegwirft
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Interessieren wuerde mich das natuerlich auch, allerdings befuerchte ich, dass ich keinereox hat geschrieben:24.01.2019 11:52:33Interessant wäre es jetzt so eine Lösung zu machen ohne das man Werte wegwirft
Ahnung davon haette, warum es am Ende funktioniert...
Ich muss gestehen, etwas neidisch auf Euer mathematisches Verstaendnis zu sein...
Auf jeden Fall bin ich sehr Dankbar, hier (wie schon oft) eine Loesung fuer mein Problem gefunden zu haben.
Falls Ihr Euch hier weiterhin mathematische Formeln um die Ohren hauen moechtet, werde ich natuerlich
mit Begeisterung mitlesen und versuchen etwas daraus zu lernen...
Mit der derzeitigen Version habe ich mal etwas herumgespielt:
Das Programm ist in C geschrieben.
Startbedingung ist:
20000 Stellen in einer ca. 2 MB. grossen .txt Datei, durch die berechneten Werte zu ersetzen.
Code: Alles auswählen
translate <[>Code: Alles auswählen
translate <-91.9506 , -9.98181 , -20.8027>Bei der Berechnung in 3D werden im Schnitt 18200 erzeugte Werte (rX, rY, rZ) verworfen.
Die Laufzeit des Programms liegt im Schnitt zwischen 0.08 bis 0.1 sek.
Das Ergebnis sieht immer perfekt gleichverteilt aus.
Gruss, heinz
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Für 2D:heinz hat geschrieben:24.01.2019 16:07:4420000 Stellen
...
Bei der Berechnung in 2D werden im Schnitt 5470 erzeugte Werte (rX, rY) verworfen.
Bei der Berechnung in 3D werden im Schnitt 18200 erzeugte Werte (rX, rY, rZ) verworfen.
Der Kreis mit Radius 1 hat die Fläche pi*1^2=pi. Das Quadrat [-1,1]x[-1,1] hat die Fläche 2*2=4. Es werden die weggeworfen, die nicht im Kreis sind. Für 20000 im Kreis braucht man 4/pi mal so viele Schüsse ins Quadrat, also etwa 25500, macht etwa 5500 zu erwartende Verworfene. 5470 passt.
Für 3D:
Die Kugel mit Radius 1 hat Volumen 4/3*pi*1^3=4/3*pi (Achtung! Gerechnet wird von links nach rechts. (4/3)*pi und 4/(3*pi) ist nicht dasselbe.). Der Würfel [-1,1]x[-1,1]x[-1,1] hat Volumen 2^3=8. Es werden die weggeworfen, die nicht in der Kugel sind. Für 20000 in der Kugel braucht man 8/(4/3*pi) Schüsse in den Würfel, also etwa 38200, macht etwa 18200 zu erwartende Verworfene. 18200 passt.
Wozu will hier jemand eine Lösung haben, wo man keine Werte verliert? Es geht bei 3D um "die Hälfte wirft man weg". Dafür würde ich keinen Tamtam machen.
Früher, als man noch nicht mal so einfach ein paar Millionen mal schießen konnte, hat man solche Probleme umgeformt, und kam dann oft nur bis zu etwas, über das es Tabellen gab. Dabei hatte man dann oft immernoch einen Approximationsfehler. Das ist heute gar nicht mehr nötig, und bei Approximationsfehler ist Montecarlo sogar besser.
Ich verstehe ja, dass das die Leute ärgert, die noch gelernt haben, wie man das umformen muss, um die Tabelle benutzen zu können. Die Generation, die noch keine Computer hatte, ist heute schon lange im Ruhestand. Es ist jetzt die nächste Generation, die noch etwas gegen Montecarlo hat, weil deren Lehrer ihnen erzählt haben, dass das Banausentum sei.
Mir hat mal ein uralter Mathematiker erzählt, dass die Banausen bevor es Computer gab mit 80g-Papier, Schere und Feinwaage integriert hätten.
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Weil es vielleicht interessant ist genau dieses Problem zu lösenLohengrin hat geschrieben:24.01.2019 23:06:06Wozu will hier jemand eine Lösung haben, wo man keine Werte verliert?
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Weil Montecarlo "Brute Force", also unelegant ist, wie mein (natürlich hinkender) Vergleich mit dem Paintballgewehr und der Zielscheibe zeigen sollte.Lohengrin hat geschrieben:24.01.2019 23:06:06Wozu will hier jemand eine Lösung haben, wo man keine Werte verliert? Es geht bei 3D um "die Hälfte wirft man weg". Dafür würde ich keinen Tamtam machen.
Den Algorithmus nutzt du nur, weil er mit moderner Rechentechnik vermeintlich billig ist. Das mag isoliert betrachtet richtig sein, aber weil alle so denken haben wir heute haufenweise Software-Bloat für den wir gigabyteweise RAM brauchen, nur um Briefe zu schreiben.
Ich hatte Spaß am Suchen nach einer Lösung, die nicht auf Quadrate schießt, wenn man Kreise treffen will. U.a. dank deiner Erklärungen habe ich auch verstanden, wo die Probleme der vorgestellten Implementierungen liegen. Ich glaube qualitativ verstanden zu haben, was man tun müsste, um den ursprünglichen Winkelansatz zum Ziel zu führen. Leider kann ich keine Lösung präsentieren, da ich mich seit jeher mit der mathematischen Formulierung von Lösungen schwer tue.
@heinz:
Mich würde abschließend noch interessieren, wozu du das brauchst. Als es noch um Kreise und Ellipsen ging, dachte ich, du willst Galaxien für dein Weltraumspiel erzeugen. Aber wozu sind die Kugeln? Kugelsternhaufen?
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Da ist aber die frage, ob eine Galaxie eine isotrope Verteilung hat. Ich würde jetzt ad-hoc sagen die Verteilung ist zur mitte hin dichter.hikaru hat geschrieben:25.01.2019 09:23:26Als es noch um Kreise und Ellipsen ging, dachte ich, du willst Galaxien für dein Weltraumspiel erzeugen.
Schon wieder eine Baustelle
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Und die zur Mitte stürzenden Massen stürzen ja nicht geradewegs auf das Zentrum zu sondern folgen der Raumkrümmung, was letztlich zu einem Drehimpuls der Galaxie führt. Am Ende hat man durch den Drehimpuls und die resultierenden Zentripedalkräfte eine hübsche Scheibenform. Und selbst in so einer Scheibe kommt es zu anisotropen Massenverdichtungen, was zur Bildung von gekrümmten "Speichen" führt, den Spiralarmen....reox hat geschrieben:25.01.2019 09:39:13Ich würde jetzt ad-hoc sagen die Verteilung ist zur mitte hin dichter.
OK, genug Physik für heute.
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Die Entstehungsgeschichte:hikaru hat geschrieben:25.01.2019 09:23:26@heinz:
Mich würde abschließend noch interessieren, wozu du das brauchst.
Ich habe zu Weihnachten einen Nikolaus in Pov erstellt der in einem Wald stehen sollte.
Also musste ich die Baeume so um ihn herum verteilen das keiner zwischen Kamera und Nikolaus steht und sich alle innerhalb eines kreisfoermigen Horizontes befinden.
Von Hand, eine Sisyphusaufgabe...
Da ich Computer mag und gerne Programmiere schrieb ich mir also ein Programm mit dem ich in der POV-Datei einzelne Zeichen durch Zufallswerte ersetzen konnte.
Das hab ich dann einfach so oft laufenlassen bis es gepasst hat.
Als ich dann spaeter im Bett lag, (im Bett hab ich immer gute Ideen...) dachte ich mir, es waere doch praktisch ein Programm zu haben welches
die Koordinaten gleich Kreisfoermig korrekt verteilen kann und das man auf alle Arten von ASCI-Dateien "loslassen" kann.
Sowas wie >tr<, nur mit Zufallszahlen...
Und daraus entstand dann die Idee es auch gleich in 3D zu machen, da ich bis jetzt nur "2D-Sachen" Programmiert hatte.
Mein Weltraumspiel ruht z.Z. etwas... Aber ich habe auch schon einiges geschafft.hikaru hat geschrieben:25.01.2019 09:23:26Als es noch um Kreise und Ellipsen ging, dachte ich, du willst Galaxien für dein Weltraumspiel erzeugen. Aber wozu sind die Kugeln? Kugelsternhaufen?
Man kann z.B. schon in der Galaxis "rumfliegen" (65536 * 65536 = 4294967296 Sektoren. Davon ca. 20000000 Sternsysteme mit bis zu 10 Planeten.)
Es gibt einen Pilot der Luft, Nahrung und normale Temperaturen braucht.
Man kann schon Materialien auf den Planeten mittels einer Sonde abbauen, das Schiff an Gasplaneten auftanken, aus den Rohstoffen "Dinge herstellen",
die Energieverteilung einstellen, das Schiff reparieren und noch einiges mehr.
Es fehlt aber auch noch sehr viel. Der Aufwand ist "ziemlich Riesig".
Alle Animationen sind mit POV erstellt, Grafiken meist mit Gimp oder Inkscape. Die gesamte Vertonung fehlt noch komplett, usw. usf.
Der Code ist eine Mischung aus C und C++, fuer die Garfik nutze ich SDL.
Es war irgendwie schon immer eine Art "Traum" von mir mal ein Weltraumspiel zu machen.
Ich hoffe ich bekomme es irgendwann fertig...
Gruss, heinz
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Der andere Weg ist mit Rechnerei verbunden.hikaru hat geschrieben:25.01.2019 09:23:26Den Algorithmus nutzt du nur, weil er mit moderner Rechentechnik vermeintlich billig ist.
Wenn man Radius vom Raumwinkel abtrennt, muss man, um den Radius zu wählen, dritte Wurzel ziehen. Wenn man dann noch den Raumwinkel in phi und theta zerlegt, muss man, um theta zu wählen, asin rechnen. Und dann nochmal sin und cos, um das wieder in kartesischen Koordinaten zu haben, die man dann plotten kann.
Ich weiß nicht, wie aufwendig das Erzeugen von Zufallszahlen ist. Wenn ich besonders zufällige Zufallszahlen haben will, würde ich die Rechnerei in Kauf nehmen, um die Anzahl der Schüsse nicht zu verdoppeln.
Ich halte den Winkelansatz für unnötig kompliziert. Das wäre sinnvoll, wenn der Radius vom Raumwinkel getrennt sein soll, und wenn es eine bevorzugte Achse gibt, zB weil das Ding um die Polachse rotiert.hikaru hat geschrieben:25.01.2019 09:23:26Ich glaube qualitativ verstanden zu haben, was man tun müsste, um den ursprünglichen Winkelansatz zum Ziel zu führen.
Es sollen kartesische Koordinaten geplottet werden, also erzeuge ich möglichst einfach kartesische Koordinaten.
Ein Hau-Ruck-Verfahren zur Erzeugung einer Gleichverteilung in der Einheitskugel, ohne daneben schießen zu müssen, wäre, erst x, dann y und dann z zu wählen.
Für x brauche ich einen Zufallsgenerator, der etwas zwischen -1 und 1 ausgibt, und dessen Dichte proportional zur Fläche des Schnittes der Einheitskugel bei x ist, also Dichte proportional zu 1-x^2. Die Dichte muss man integrieren und die Konstanten so wählen, dass es die Verteilungsfunktion eines Wahrscheinlichkeitsmaßes wird. Die Umkehrfunktion der Verteilungsfunktion ist das Passende, was aus auf 0 bis 1 gleichverteilten Zufallszahlen x macht.
Dann kommt die y-Koordinate des Punktes, der in dieser Schnittfläche der Einheitskugel liegt (ein Kreis mit Radius 1-x^2). Die Dichte muss in der Mitte proportional zu Wurzel(1-x^2-y^2) sein, davor und dahinter 0. Integriert wird das irgendwas Wildes mit asin. Und umkehren muss man das dann auch noch.
Dann kommt die z-Koordinate dran. Das ist dann gleichverteilt zwischen minus und plus Wurzel(1-x^2-y^2).
Harry, hol schon mal das Rasiermesser!
Re: Probleme beim Zufalls-Punkte erzeugen [gelöst]
Ich glaube, ich hätte den Nikolaus auf ein Feld gestellt.heinz hat geschrieben:25.01.2019 13:44:43Ich habe zu Weihnachten einen Nikolaus in Pov erstellt der in einem Wald stehen sollte.
Also musste ich die Baeume so um ihn herum verteilen das keiner zwischen Kamera und Nikolaus steht und sich alle innerhalb eines kreisfoermigen Horizontes befinden.
Von Hand, eine Sisyphusaufgabe...
Schön, dass du da etwas hartnäckiger warst!
Klingt ein wenig nach "Elite". Dass der Aufwand riesig ist kann ich mir vorstellen.heinz hat geschrieben:25.01.2019 13:44:43Mein Weltraumspiel ruht z.Z. etwas... Aber ich habe auch schon einiges geschafft.
Man kann z.B. schon in der Galaxis "rumfliegen" (65536 * 65536 = 4294967296 Sektoren. Davon ca. 20000000 Sternsysteme mit bis zu 10 Planeten.)
Es gibt einen Pilot der Luft, Nahrung und normale Temperaturen braucht.
Man kann schon Materialien auf den Planeten mittels einer Sonde abbauen, das Schiff an Gasplaneten auftanken, aus den Rohstoffen "Dinge herstellen",
die Energieverteilung einstellen, das Schiff reparieren und noch einiges mehr.
Es fehlt aber auch noch sehr viel. Der Aufwand ist "ziemlich Riesig".
Wahrscheinlich wirst du nie wirklich "fertg" werden, weil dir in einer offenen Spielwelt immer noch mehr einfallen wird.
Da hast du natürlich recht. Rechnen muss man bei beiden Varianten und den Aufwand müsste man dann gegeneinander abwägen. Ich finde es nur konzeptuell hässlich, Punkte zu erzeugen, von denen man von Anfang an weiß, dass man sie man gar nicht braucht.Lohengrin hat geschrieben:25.01.2019 18:48:01Der andere Weg ist mit Rechnerei verbunden.
Wenn man Radius vom Raumwinkel abtrennt, muss man, um den Radius zu wählen, dritte Wurzel ziehen. Wenn man dann noch den Raumwinkel in phi und theta zerlegt, muss man, um theta zu wählen, asin rechnen. Und dann nochmal sin und cos, um das wieder in kartesischen Koordinaten zu haben, die man dann plotten kann.
Ich weiß nicht, wie aufwendig das Erzeugen von Zufallszahlen ist. Wenn ich besonders zufällige Zufallszahlen haben will, würde ich die Rechnerei in Kauf nehmen, um die Anzahl der Schüsse nicht zu verdoppeln.
Ich glaube, ein Grund warum mir der Montecarlo-Ansatz nicht gefällt ist, dass er mit steigender Dimensionszahl immer ineffizienter wird, weil das n-Volumen der n-Kugel im Vergleich zum n-Volumen des n-Kubus immer kleiner wird.
Das und der Umstand, dass wir dazu nun eine funktionierende Lösung haben ist eigentlich das Einzige, was mich von dem Ansatz überzeugt: "It gets the job done."Lohengrin hat geschrieben:25.01.2019 18:48:01Es sollen kartesische Koordinaten geplottet werden, also erzeuge ich möglichst einfach kartesische Koordinaten.
Da stellt sich mir im Anschluss aber gleich die Frage, ob eine Kugel hier wirklich gebraucht wird, oder ob es nicht auch ein Kubus täte. Ich vermute, den Unterschied würde heinz in der letztendlich generierten Szene gar nicht sehen.