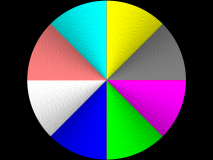
Gezeichnet wurden immer wieder Kreise, bei denen der Radius jedes mal um 1 erhöht wurde.
Wie man sieht, werden hier sehr viele Pixel nicht gezeichnet.
Was ich suche ist ein Algo. der diese leerstellen nicht hat.
gruß heinz
Du musst ganz genau das tun, was Du sowieso tun musst. Ein Sektor, den Du nicht nach dem Gesuchten durchsuchst, ist in diesem Fall ja mal *gar nichts* wert. In den Container tust Du nur die Sektoren bzw. Systeme, die Du gefunden hast. Und mit dem richtigen Container, werden die „automatisch“ nach dem sortiert, was Du brauchst. Am Ende einer „Flood-Fill-Orgie“ guckst Du, ob in dem Container etwas drin ist. Wenn ja, ist es das erste Element, wenn nicht, nimmst Du Dir den nächsten „Suchradius“ vor. Fäddich.heinz hat geschrieben:13.04.2018 19:11:25Dazu müsste ich aber doch auch erst alle Systeme berechnen/erstellen um sie in die Container legen zu können...GregorS hat geschrieben:13.04.2018 18:51:55Nimm einen Container, der nach der Entfernung zum Schiff sortiert. Wenn es mehrere Fundstellen gibt, befindet sich das gesuchte Ding an der ersten Position.
Klasse! Ich glaube mal Du bist der erste, der wirklich verstanden hat worum es mir geht.tobo hat geschrieben:13.04.2018 19:37:08Wie ich das verstehe: Du suchst nicht den Kreis, sondern die Kreislinie. Auf dieser Linie (1 mal rumgelaufen; Symmetrie 1/8) schaust du dir die Informationen der dabei jeweils betretenen Felder/Pixel an. Ist auf keinem dieser Felder die Information vorhanden, dann Radius+1 und laufe die nächstgrößere Kreislinie ab. Problem dabei, du willst natürlich keine Felder auslassen, du darfst aber auch keine Felder doppelt betreten, da die Information dieser Felder dynamisch generiert wird und deswegen variiert. Passt das so in etwa?
Nein, ich schau gleich mal rein. Danke...tobo hat geschrieben:13.04.2018 19:37:08Nebenbei, kennst du das schon?
http://www.mttcs.org/Skripte/Pra/Materi ... esung9.pdf
Ich möchte eigentlich, wenn möglich, garnichts irgenwo reintun um es hinterher abzusuchen/abzufragen. (Zu viele "unnütz" abgesuchte Felder...)GregorS hat geschrieben:13.04.2018 19:36:07...In den Container tust Du nur die Sektoren bzw. Systeme, die Du gefunden hast.
Mannomann ... dann tu die gefundenen Sektoren/Systeme (also DIE, DIE DAS ENTHALTEN, WAS DU SUCHST) halt sonstwo rein. Hauptsache, Du musst nie-nie-niemals Container benutzen, was?heinz hat geschrieben:13.04.2018 19:57:23Ich möchte eigentlich, wenn möglich, garnichts irgenwo reintun um es hinterher abzusuchen/abzufragen. (Zu viele "unnütz" abgesuchte Felder...)GregorS hat geschrieben:13.04.2018 19:36:07...In den Container tust Du nur die Sektoren bzw. Systeme, die Du gefunden hast.
Was ist denn jetzt los?GregorS hat geschrieben:13.04.2018 20:07:57Mannomann ... dann tu die gefundenen Sektoren/Systeme (also DIE, DIE DAS ENTHALTEN, WAS DU SUCHST) halt sonstwo rein. Hauptsache, Du musst nie-nie-niemals Container benutzen, was?
Tja, dann ...
Also mal extra-langsam:heinz hat geschrieben:13.04.2018 20:17:00Was ist denn jetzt los?
Es geht nicht um Container sondern um Rechenaufwand.
Mit der von Dir vorgeschlagenen Methode (Flood-Fill) muss man sehr viele Sektoren berechnen, obwohl man das nächste System vlt. schon längst hat.
Anscheinend nicht. Sorry.
Man kann also erst wissen welches der nächste ist wenn man alle Fundstellen innerhalb des gefüllten Bereiches ermittelt hat.GregorS hat geschrieben:13.04.2018 20:32:45- Wenn der Bereich innerhalb des Kreises fertig durchsucht wurde, ...
Das wäre extrem klasse!bluestar hat geschrieben:13.04.2018 20:52:30Kannst du mal deinen Code posten, dann kann ich dir die Stellen zeigen, wo die Fehlpixel entstehen.
Es scheint also irgendwie zu gehen.Die hohlen Kreise geben die Pixel an, die eingefärbt werden, wenn bei d=0 das andere Pixel gewählt wird.
Doch kommt man, so zum Beispiel:tobo hat geschrieben:13.04.2018 23:06:19Trotzdem glaube ich nicht, dass du an der doppelten Strichstärke vorbeikommst!?